#74 Search a 2D Matrix

Write an efficient algorithm that searches for a value in an m x n matrix. This matrix has the following properties:

• Integers in each row are sorted from left to right.
• The first integer of each row is greater than the last integer of the previous row.

Example 1:

Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
Output: true

Example 2:

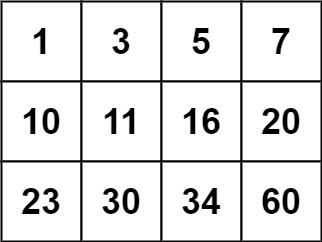
Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
Output: false

Constraints:

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 100
• -104 <= matrix[i][j], target <= 104

Solution :

bool searchMatrix(vector<vector<int>>& matrix, int target) {
        int r = matrix.size()-1;
    int c = matrix[0].size()-1;
    int i = 0;
    while(i<r && matrix[i][c] < target)
        i++;
    if(i>r)
        return false;
    for(int j=0; j<=c; j++)
    {
        if(matrix[i][j] == target)
        {
            return true;
        }
    }
    return false;

Complete Code :

// Cyclically rotate an array by one
#include <bits/stdc++.h>
using namespace std;

// Time Complexity - O(row x col)
bool searchWithBruteforce(vector<vector<int>>& matrix, int target) {
    int m = matrix.size();
    int n = matrix[0].size();
    for(int i=0; i<m; i++)
    {
        for(int j=0; j<n; j++)
        {
            if(matrix[i][j] == target)
            {
                return true;
            }
        }
    }
    return false;
}

// Time Complexity - O(row + col)
bool searchOptimized(vector<vector<int>>& matrix, int target) 
{
    int r = matrix.size()-1;
    int c = matrix[0].size()-1;
    int i = 0;
    while(i<r && matrix[i][c] < target)
        i++;
    if(i>r)
        return false;
    for(int j=0; j<=c; j++)
    {
        if(matrix[i][j] == target)
        {
            return true;
        }
    }
    return false;
}

int main()
{
	vector<vector<int>> vect = {{1,2,3,4},
				{5,6,7,8},
				{9,10,11,12}};
	if(searchOptimized(vect, 6))
        cout << "found" << endl;
    else
        cout << "not found" << endl;
	return 0;
}