1.Sliding Window
Usage: This algorithmic technique is used when we need to handle the input data in a specific window size.
DS Involved: Array, String, HashTable
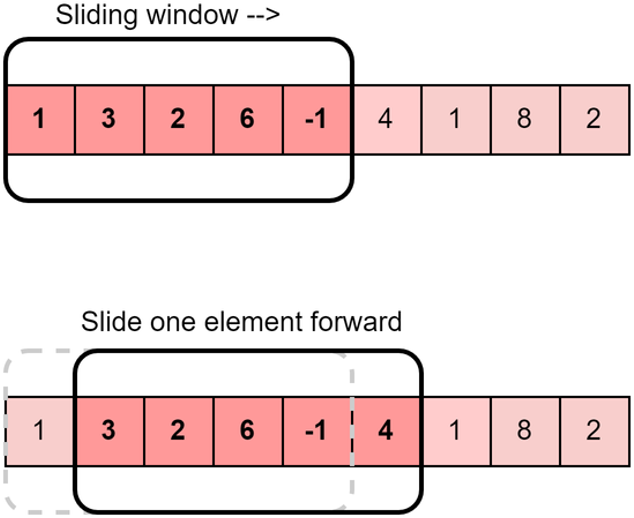
Sample Problems:
- Longest Substring with ‘K’ Distinct Characters
- Fruits into Baskets
2. Islands (Matrix Traversal)
Usage: This pattern describes all the efficient ways of traversing a matrix (or 2D array).
DS Involved: Matrix, Queue

Sample Problems:
- Number of Islands
- Flood Fill
- Cycle in a Matrix
. Two Pointers
Usage: This technique uses two pointers to iterate input data. Generally, both pointers move in the opposite direction at a constant interval.
DS Involved: Array, String, LinkedList

Sample Problems:
- Squaring a Sorted Array
- Dutch National Flag Problem
- Minimum Window Sort
4. Fast & Slow Pointers
Usage: Also known as Hare & Tortoise algorithm. This technique uses two pointers that traverse the input data at different speeds.
DS Involved: Array, String, LinkedList
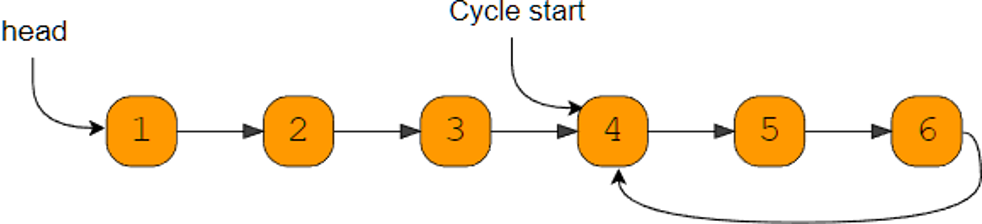
Sample Problems:
- Middle of the LinkedList
- Happy Number
- Cycle in a Circular Array
5. Merge Intervals
Usage: This technique is used to deal with overlapping intervals.
DS Involved: Array, Heap

Sample Problems:
- Conflicting Appointments
- Minimum Meeting Rooms
6. Cyclic Sort
Usage: Use this technique to solve array problems where the input data lies within a fixed range.
DS Involved: Array
Sample Problems:
- Find all Missing Numbers
- Find all Duplicate Numbers
- Find the First K Missing Positive Numbers
7. In-place Reversal of a LinkedList
Usage: This technique describes an efficient way to reverse the links between a set of nodes of a LinkedList. Often, the constraint is that we need to do this in-place, i.e., using the existing node objects and without using extra memory.
DS Involved: LinkedList
Sample Problems:
- Reverse every K-element Sub-list
- Rotate a LinkedList
8. Breadth-First Search
Usage: This technique is used to solve problems involving traversing trees or graphs in a breadth-first search manner.
DS Involved: Tree, Graph, Matrix, Queue
Sample Problems:
- Binary Tree Level Order Traversal
- Minimum Depth of a Binary Tree
- Connect Level Order Siblings
9. Depth First Search
Usage: This technique is used to solve problems involving traversing trees or graphs in a depth-first search manner.
DS Involved: Tree, Graph, Matrix
Sample Problems:
- Path With Given Sequence
- Count Paths for a Sum
10. Two Heaps
Usage: In many problems, we are given a set of elements that can be divided into two parts. We are interested in knowing the smallest element in one part and the biggest element in the other part. As the name suggests, this technique uses a Min-Heap to find the smallest element and a Max-Heap to find the biggest element.
DS Involved: Heap, Array
Sample Problems:
- Find the Median of a Number Stream
- Next Interval
11. Subsets
Usage: Use this technique when the problem asks to deal with permutations or combinations of a set of elements.
DS Involved: Queue, Array, String
Sample Problems:
- String Permutations by changing case
- Unique Generalized Abbreviations
12. Modified Binary Search
Usage: Use this technique to search a sorted set of elements efficiently.
DS Involved: Array
Sample Problems:
- Ceiling of a Number
- Bitonic Array Maximum
13. Bitwise XOR
Usage: This technique uses the XOR operator to manipulate bits to solve problems.
DS Involved: Array, Bits
Sample Problems:
- Two Single Numbers
- Flip and Invert an Image
14. Top ‘K’ Elements
Usage: This technique is used to find top/smallest/frequently occurring ‘K’ elements in a set.
DS Involved: Array, Heap, Queue
Sample Problems:
- ‘K’ Closest Points to the Origin
- Maximum Distinct Elements
15. K-way Merge
Usage: This technique helps us solve problems that involve a list of sorted arrays.
DS Involved: Array, Queue, Heap
Sample Problems:
- Kth Smallest Number in M Sorted Lists
- Kth Smallest Number in a Sorted Matrix
16. Topological Sort
Usage: Use this technique to find a linear ordering of elements that have dependencies on each other.
DS Involved: Array, HashTable, Queue, Graph
Sample Problems:
- Tasks Scheduling
- Alien Dictionary
17. 0/1 Knapsack
Usage: This technique is used to solve optimization problems. Use this technique to select elements that give maximum profit from a given set with a limitation on capacity and that each element can only be picked once.
DS Involved: Array, HashTable
Sample Problems:
- Equal Subset Sum Partition
- Minimum Subset Sum Difference
18. Fibonacci Numbers
Usage: Use this technique to solve problems that follow the Fibonacci numbers sequence, i.e., every subsequent number is calculated from the last few numbers.
DS Involved: Array, HashTable
Sample Problems:
- Staircase
- House Thief
19. Palindromic Subsequence
Usage: This technique is used to solve optimization problems related to palindromic sequences or strings.
DS Involved: Array, HashTable
Sample Problems:
- Longest Palindromic Subsequence
- Minimum Deletions in a String to make it a Palindrome
20. Longest Common Substring
Usage: Use this technique to find the optimal part of a string/sequence or set of strings/sequences.
DS Involved: Array, HashTable
Sample Problems:
- Maximum Sum Increasing Subsequence
- Edit Distance
